प्राथमिक कार्यों के मूल गुणों की तालिका। कार्य और ग्राफ़

अनुभाग में मुख्य प्राथमिक कार्यों और उनके गुणों पर संदर्भ सामग्री शामिल है। प्रारंभिक कार्यों का वर्गीकरण दिया गया है। नीचे उपखंडों के लिंक दिए गए हैं जो विशिष्ट कार्यों के गुणों पर चर्चा करते हैं - ग्राफ़, सूत्र, व्युत्पन्न, प्रतिअवकलन (अभिन्न), श्रृंखला विस्तार, जटिल चर के माध्यम से अभिव्यक्ति।

बुनियादी कार्यों के लिए संदर्भ पृष्ठ

प्राथमिक कार्यों का वर्गीकरण

बीजीय फलनएक फ़ंक्शन है जो समीकरण को संतुष्ट करता है:
,
आश्रित चर y और स्वतंत्र चर x में एक बहुपद कहाँ है। इसे इस प्रकार लिखा जा सकता है:
,
बहुपद कहाँ हैं.

बीजगणितीय कार्यों को बहुपद (संपूर्ण तर्कसंगत कार्य), तर्कसंगत कार्य और अपरिमेय कार्य में विभाजित किया गया है।

संपूर्ण तर्कसंगत कार्य, जिसे भी कहा जाता है बहुपदया बहुपद, जोड़ (घटाव) और गुणा के अंकगणितीय संचालन का उपयोग करके चर x और संख्याओं की एक सीमित संख्या से प्राप्त किया जाता है। कोष्ठक खोलने के बाद, बहुपद को विहित रूप में घटा दिया जाता है:
.

भिन्नात्मक तर्कसंगत कार्य, या केवल तर्कसंगत कार्य, जोड़ (घटाव), गुणा और भाग के अंकगणितीय संचालन का उपयोग करके चर x और संख्याओं की एक सीमित संख्या से प्राप्त किया जाता है। तर्कसंगत फ़ंक्शन को फॉर्म में घटाया जा सकता है
,
कहाँ और बहुपद हैं.

तर्कहीन कार्यएक बीजीय फलन है जो तर्कसंगत नहीं है। एक नियम के रूप में, एक अपरिमेय कार्य को जड़ों और उनकी रचनाओं को तर्कसंगत कार्यों के रूप में समझा जाता है। घात n के मूल को समीकरण के समाधान के रूप में परिभाषित किया गया है
.
इसे इस प्रकार नामित किया गया है:
.

पारलौकिक कार्यगैर-बीजीय फलन कहलाते हैं। ये घातांकीय, त्रिकोणमितीय, अतिशयोक्तिपूर्ण और उनके व्युत्क्रम फलन हैं।

बुनियादी प्राथमिक कार्यों का अवलोकन

सभी प्रारंभिक कार्यों को प्रपत्र की अभिव्यक्ति पर किए गए जोड़, घटाव, गुणा और भाग संचालन की एक सीमित संख्या के रूप में दर्शाया जा सकता है:
जेड टी .
व्युत्क्रम फलनों को लघुगणक के रूप में भी व्यक्त किया जा सकता है। बुनियादी प्राथमिक कार्य नीचे सूचीबद्ध हैं।

ऊर्जा समीकरण :
y(x) = x p ,
जहाँ p घातांक है। यह डिग्री x के आधार पर निर्भर करता है.
पावर फ़ंक्शन का व्युत्क्रम भी पावर फ़ंक्शन है:
.
घातांक पी के पूर्णांक गैर-नकारात्मक मान के लिए, यह एक बहुपद है। पूर्णांक मान p के लिए - एक तर्कसंगत कार्य। तर्कसंगत अर्थ के साथ - एक तर्कहीन कार्य।

पारलौकिक कार्य

घातांक प्रकार्य :
y(x) = a x ,
जहां a डिग्री का आधार है। यह घातांक x पर निर्भर करता है।
व्युत्क्रम फलन आधार a का लघुगणक है:
एक्स = एक y लॉग इन करें.

घातांक, ई से एक्स घात:
y(x) = e x ,
यह एक घातीय फलन है जिसका व्युत्पन्न स्वयं फलन के बराबर है:
.
घातांक का आधार संख्या e है:
≈ 2,718281828459045... .
व्युत्क्रम फलन प्राकृतिक लघुगणक है - संख्या ई के आधार का लघुगणक:
एक्स = एलएन वाई ≡ लॉग ई वाई.

त्रिकोणमितीय कार्य:
साइन: ;
कोसाइन: ;
स्पर्शरेखा: ;
कोटैंजेंट: ;
यहाँ i काल्पनिक इकाई है, i 2 = -1.

व्युत्क्रम त्रिकोणमितीय फलन:
आर्कसाइन: एक्स = आर्क्सिन वाई, ;
चाप कोज्या: x = आर्ककोस वाई, ;
आर्कटिक: x = आर्कटान वाई, ;
चाप स्पर्शरेखा: x = आर्कसीटीजी वाई, .

बुनियादी प्राथमिक कार्यहैं: स्थिर कार्य (स्थिर), जड़ एन-वीं डिग्री, पावर फ़ंक्शन, घातांक, लॉगरिदमिक फ़ंक्शन, त्रिकोणमितीय और व्युत्क्रम त्रिकोणमितीय फ़ंक्शन।

स्थायी कार्य.

सूत्र द्वारा सभी वास्तविक संख्याओं के समुच्चय पर एक स्थिर फलन दिया जाता है, जहाँ सी– कुछ वास्तविक संख्या. एक स्थिर फ़ंक्शन स्वतंत्र चर के प्रत्येक वास्तविक मान को निर्दिष्ट करता है एक्सआश्रित चर का समान मान य- अर्थ साथ. एक स्थिर फलन को स्थिरांक भी कहा जाता है।

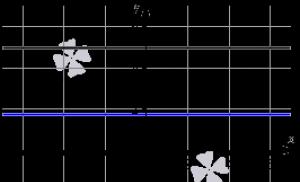
एक स्थिर फलन का ग्राफ x-अक्ष के समानांतर और निर्देशांक वाले बिंदु से गुजरने वाली एक सीधी रेखा है (0,सी). उदाहरण के लिए, आइए स्थिर फलनों के ग्राफ़ दिखाएं y=5,y=-2और, जो नीचे दिए गए चित्र में क्रमशः काली, लाल और नीली रेखाओं के अनुरूप है।

एक स्थिर फलन के गुण.

डोमेन: वास्तविक संख्याओं का संपूर्ण सेट.

अचर फलन सम है.

मानों की सीमा: एक एकल संख्या से युक्त सेट साथ.

एक स्थिर फलन न तो बढ़ता है और न ही घटता है (इसीलिए यह स्थिर है)।

किसी स्थिरांक की उत्तलता और अवतलता के बारे में बात करने का कोई मतलब नहीं है।

कोई स्पर्शोन्मुख नहीं हैं.

फ़ंक्शन बिंदु से होकर गुजरता है (0,सी)विमान का समन्वय।

nवीं डिग्री की जड़.

आइए मूल प्राथमिक फ़ंक्शन पर विचार करें, जो सूत्र द्वारा दिया गया है, जहां एन- एक से बड़ी प्राकृतिक संख्या।

nवाँ मूल, n एक सम संख्या है।

आइए रूट फ़ंक्शन से शुरू करें एनमूल घातांक के सम मानों के लिए -वीं शक्ति एन.

उदाहरण के तौर पर, यहां फ़ंक्शन ग्राफ़ की छवियों वाला एक चित्र है और, वे काली, लाल और नीली रेखाओं के अनुरूप हैं।

सम-डिग्री रूट फ़ंक्शंस के ग्राफ़ में घातांक के अन्य मानों के लिए समान उपस्थिति होती है।

रूट फ़ंक्शन के गुणएन -सम के लिए शक्तिएन .

nवाँ मूल, n एक विषम संख्या है।

मूल कार्य एनएक विषम मूल घातांक के साथ -वीं शक्ति एनवास्तविक संख्याओं के संपूर्ण सेट पर परिभाषित किया गया है। उदाहरण के लिए, यहां फ़ंक्शन ग्राफ़ हैं और, वे काले, लाल और नीले वक्रों के अनुरूप हैं।

बुनियादी प्राथमिक कार्य, उनके अंतर्निहित गुण और संबंधित ग्राफ गणितीय ज्ञान की बुनियादी बातों में से एक हैं, जो गुणन तालिका के महत्व के समान हैं। प्राथमिक कार्य सभी सैद्धांतिक मुद्दों के अध्ययन का आधार, समर्थन हैं।

Yandex.RTB R-A-339285-1

नीचे दिया गया लेख बुनियादी प्राथमिक कार्यों के विषय पर मुख्य सामग्री प्रदान करता है। हम शब्दों का परिचय देंगे, उनकी परिभाषाएँ देंगे; आइए प्रत्येक प्रकार के प्राथमिक कार्यों का विस्तार से अध्ययन करें और उनके गुणों का विश्लेषण करें।

निम्नलिखित प्रकार के बुनियादी प्राथमिक कार्य प्रतिष्ठित हैं:

परिभाषा 1

• स्थिर कार्य (स्थिर);
• nवीं जड़;
• ऊर्जा समीकरण;
• घातांक प्रकार्य;
• लघुगणकीय कार्य;
• त्रिकोणमितीय कार्य;
• भ्रातृ त्रिकोणमितीय फलन.

एक स्थिर फलन को सूत्र द्वारा परिभाषित किया जाता है: y = C (C एक निश्चित वास्तविक संख्या है) और इसका एक नाम भी है: स्थिरांक। यह फ़ंक्शन स्वतंत्र चर x के किसी भी वास्तविक मान और चर y के समान मान - C का मान के अनुरूपता निर्धारित करता है।

स्थिरांक का ग्राफ़ एक सीधी रेखा है जो भुज अक्ष के समानांतर है और निर्देशांक (0, C) वाले बिंदु से होकर गुजरती है। स्पष्टता के लिए, हम स्थिर फलनों y = 5, y = - 2, y = 3, y = 3 (चित्र में क्रमशः काले, लाल और नीले रंग में दर्शाए गए) के ग्राफ प्रस्तुत करते हैं।

परिभाषा 2

इस प्राथमिक फ़ंक्शन को सूत्र y = x n द्वारा परिभाषित किया गया है (n एक से बड़ी प्राकृतिक संख्या है)।

आइए फ़ंक्शन के दो रूपों पर विचार करें।

1. nवाँ मूल, n - सम संख्या

स्पष्टता के लिए, हम एक चित्र दर्शाते हैं जो ऐसे कार्यों के ग्राफ़ दिखाता है: y = x, y = x 4 और y = x8. ये विशेषताएँ रंग कोडित हैं: क्रमशः काला, लाल और नीला।

सम डिग्री के फ़ंक्शन के ग्राफ़ में घातांक के अन्य मानों के लिए समान उपस्थिति होती है।

परिभाषा 3

nवें मूल फलन के गुण, n एक सम संख्या है

• परिभाषा का क्षेत्र - सभी गैर-नकारात्मक वास्तविक संख्याओं का सेट [ 0 , + ∞) ;
• जब x = 0, फलन y = x n का मान शून्य के बराबर है;
• यह फलन सामान्य रूप का फलन है (यह न तो सम है और न ही विषम);
• रेंज: [ 0 , + ∞) ;
• यह फलन y = x n सम मूल घातांक के साथ परिभाषा के संपूर्ण क्षेत्र में बढ़ता है;
• फ़ंक्शन में परिभाषा के पूरे क्षेत्र में ऊपर की दिशा के साथ एक उत्तलता है;
• कोई विभक्ति बिंदु नहीं हैं;
• कोई स्पर्शोन्मुख नहीं हैं;
• सम n के लिए फ़ंक्शन का ग्राफ़ बिंदुओं (0; 0) और (1; 1) से होकर गुजरता है।

1. nवाँ मूल, n - विषम संख्या

ऐसा फ़ंक्शन वास्तविक संख्याओं के संपूर्ण सेट पर परिभाषित किया गया है। स्पष्टता के लिए, फ़ंक्शन के ग्राफ़ पर विचार करें y = x 3 , y = x 5 और x 9 . चित्र में उन्हें रंगों द्वारा दर्शाया गया है: काला, लाल और नीला क्रमशः वक्रों के रंग हैं।

फ़ंक्शन y = x n के मूल घातांक के अन्य विषम मान एक समान प्रकार का ग्राफ़ देंगे।

परिभाषा 4

nवें मूल फलन के गुण, n एक विषम संख्या है

• परिभाषा का क्षेत्र - सभी वास्तविक संख्याओं का समुच्चय;
• यह फ़ंक्शन अजीब है;
• मानों की श्रेणी - सभी वास्तविक संख्याओं का समुच्चय;
• विषम मूल घातांक के लिए फ़ंक्शन y = x n परिभाषा के संपूर्ण क्षेत्र में बढ़ता है;
• फ़ंक्शन में अंतराल पर उत्तलता है (- ∞ ; 0 ] और अंतराल पर उत्तलता है [ 0 , + ∞);
• विभक्ति बिंदु के निर्देशांक (0; 0) हैं;
• कोई स्पर्शोन्मुख नहीं हैं;
• विषम n के लिए फ़ंक्शन का ग्राफ बिंदुओं (- 1 ; - 1), (0 ; 0) और (1 ; 1) से होकर गुजरता है।

ऊर्जा समीकरण

पावर फ़ंक्शन को सूत्र y = x a द्वारा परिभाषित किया गया है।

ग्राफ़ की उपस्थिति और फ़ंक्शन के गुण घातांक के मान पर निर्भर करते हैं।

• जब किसी पावर फ़ंक्शन में पूर्णांक घातांक a होता है, तो पावर फ़ंक्शन के ग्राफ़ का प्रकार और उसके गुण इस पर निर्भर करते हैं कि घातांक सम है या विषम, साथ ही घातांक के पास कौन सा चिह्न है। आइए नीचे इन सभी विशेष मामलों पर अधिक विस्तार से विचार करें;
• घातांक भिन्नात्मक या अपरिमेय हो सकता है - इसके आधार पर, ग्राफ़ के प्रकार और फ़ंक्शन के गुण भी भिन्न होते हैं। हम कई शर्तें निर्धारित करके विशेष मामलों का विश्लेषण करेंगे: 0< a < 1 ; a > 1 ; - 1 < a < 0 и a < - 1 ;
• एक पावर फ़ंक्शन में शून्य घातांक हो सकता है; हम इस मामले का नीचे और अधिक विस्तार से विश्लेषण भी करेंगे।

आइए पावर फ़ंक्शन का विश्लेषण करें y = x a, जब a एक विषम धनात्मक संख्या है, उदाहरण के लिए, a = 1, 3, 5...

स्पष्टता के लिए, हम ऐसे पावर फ़ंक्शंस के ग्राफ़ दर्शाते हैं: y = x (ग्राफिक रंग काला), y = x 3 (ग्राफ़ का नीला रंग), y = x 5 (ग्राफ़ का लाल रंग), y = x 7 (ग्राफिक रंग हरा)। जब a = 1, हमें रैखिक फलन y = x प्राप्त होता है।

परिभाषा 6

घातांक के विषम धनात्मक होने पर घात के गुण कार्य करते हैं

• फ़ंक्शन x ∈ (- ∞ ; + ∞) के लिए बढ़ रहा है;
• फ़ंक्शन में x ∈ (- ∞ ; 0 ] के लिए उत्तलता है और x ∈ [ 0 ; + ∞) के लिए अवतलता है (रैखिक फ़ंक्शन को छोड़कर);
• विभक्ति बिंदु के निर्देशांक (0 ; 0) हैं (रैखिक फ़ंक्शन को छोड़कर);
• कोई स्पर्शोन्मुख नहीं हैं;
• फ़ंक्शन के पारित होने के बिंदु: (- 1 ; - 1) , (0 ; 0) , (1 ; 1) .

आइए पावर फ़ंक्शन का विश्लेषण करें y = x a, जब a एक सम धनात्मक संख्या है, उदाहरण के लिए, a = 2, 4, 6...

स्पष्टता के लिए, हम ऐसे शक्ति कार्यों के ग्राफ़ दर्शाते हैं: y = x 2 (ग्राफिक रंग काला), y = x 4 (ग्राफ़ का नीला रंग), y = x 8 (ग्राफ़ का लाल रंग)। जब a = 2 होता है, तो हमें एक द्विघात फलन प्राप्त होता है, जिसका ग्राफ एक द्विघात परवलय होता है।

परिभाषा 7

घातांक के सम धनात्मक होने पर घात फलन के गुण:

• परिभाषा का क्षेत्र: x ∈ (- ∞ ; + ∞) ;
• x ∈ (- ∞ ; 0 ] ) के लिए घट रहा है;
• फ़ंक्शन में x ∈ (- ∞ ; + ∞) के लिए अवतलता है;
• कोई विभक्ति बिंदु नहीं हैं;
• कोई स्पर्शोन्मुख नहीं हैं;
• फ़ंक्शन के पारित होने के बिंदु: (- 1 ; 1) , (0 ; 0) , (1 ; 1) .

नीचे दिया गया चित्र पावर फ़ंक्शन ग्राफ़ के उदाहरण दिखाता है y = x a जब a एक विषम ऋणात्मक संख्या है: y = x - 9 (ग्राफिक रंग काला); y = x - 5 (ग्राफ़ का नीला रंग); y = x - 3 (ग्राफ़ का लाल रंग); y = x - 1 (ग्राफिक रंग हरा)। जब a = - 1, हम व्युत्क्रम आनुपातिकता प्राप्त करते हैं, जिसका ग्राफ एक अतिपरवलय है।

परिभाषा 8

घातांक के विषम ऋणात्मक होने पर घात फलन के गुण:

जब x = 0 होता है, तो हमें दूसरे प्रकार की असंततता प्राप्त होती है, क्योंकि lim x → 0 - 0 x a = - ∞, lim x → 0 + 0 x a = + ∞ a = - 1, - 3, - 5, ... के लिए। इस प्रकार, सीधी रेखा x = 0 एक ऊर्ध्वाधर अनंतस्पर्शी है;

• रेंज: y ∈ (- ∞ ; 0) ∪ (0 ; + ∞) ;
• फलन अजीब है क्योंकि y (- x) = - y (x);
• x ∈ - ∞ के लिए फलन घट रहा है; 0 ∪ (0 ; + ∞) ;
• फ़ंक्शन में x ∈ (- ∞ ; 0) के लिए उत्तलता और x ∈ (0 ; + ∞) के लिए अवतलता है;
• कोई विभक्ति बिंदु नहीं हैं;

k = lim x → ∞ x a x = 0, b = lim x → ∞ (x a - k x) = 0 ⇒ y = k x + b = 0, जब a = - 1, - 3, - 5,। . . .

• फ़ंक्शन के पारित होने के बिंदु: (- 1 ; - 1) , (1 ; 1) .

नीचे दिया गया चित्र पावर फ़ंक्शन y = x a के ग्राफ़ के उदाहरण दिखाता है जब a एक सम ऋणात्मक संख्या है: y = x - 8 (ग्राफिक रंग काला); y = x - 4 (ग्राफ़ का नीला रंग); y = x - 2 (ग्राफ़ का लाल रंग)।

परिभाषा 9

घातांक सम ऋणात्मक होने पर घात फलन के गुण:

• परिभाषा का क्षेत्र: x ∈ (- ∞ ; 0) ∪ (0 ; + ∞) ;

जब x = 0 होता है, तो हमें दूसरे प्रकार की असंततता प्राप्त होती है, क्योंकि a = - 2, - 4, - 6, के लिए lim x → 0 - 0 x a = + ∞, lim x → 0 + 0 x a = + ∞। इस प्रकार, सीधी रेखा x = 0 एक ऊर्ध्वाधर अनंतस्पर्शी है;

• फलन सम है क्योंकि y(-x) = y(x);
• फ़ंक्शन x ∈ (- ∞ ; 0) के लिए बढ़ रहा है और x ∈ 0 के लिए घट रहा है; + ∞ ;
• फ़ंक्शन में x ∈ (- ∞ ; 0) ∪ (0 ; + ∞) पर अवतलता है;
• कोई विभक्ति बिंदु नहीं हैं;
• क्षैतिज अनंतस्पर्शी - सीधी रेखा y = 0, क्योंकि:

k = lim x → ∞ x a x = 0 , b = lim x → ∞ (x a - k x) = 0 ⇒ y = k x + b = 0 जब a = - 2 , - 4 , - 6 , . . . .

• फ़ंक्शन के पारित होने के बिंदु: (- 1 ; 1) , (1 ; 1) .

शुरू से ही, निम्नलिखित पहलू पर ध्यान दें: ऐसे मामले में जब एक विषम हर के साथ एक सकारात्मक अंश है, कुछ लेखक इस पावर फ़ंक्शन की परिभाषा के क्षेत्र के रूप में अंतराल - ∞ लेते हैं; + ∞ , यह निर्धारित करते हुए कि घातांक a एक अप्रासंगिक भिन्न है। फिलहाल, बीजगणित और विश्लेषण के सिद्धांतों पर कई शैक्षिक प्रकाशनों के लेखक शक्ति कार्यों को परिभाषित नहीं करते हैं, जहां घातांक तर्क के नकारात्मक मूल्यों के लिए एक विषम हर के साथ एक अंश है। नीचे हम बिल्कुल इस स्थिति का पालन करेंगे: हम सेट लेंगे [ 0 ; + ∞) . छात्रों के लिए अनुशंसा: असहमति से बचने के लिए इस बिंदु पर शिक्षक के दृष्टिकोण का पता लगाएं।

तो, आइए पावर फ़ंक्शन को देखें y = x a, जब घातांक एक परिमेय या अपरिमेय संख्या है, बशर्ते कि 0< a < 1 .

आइए हम ग्राफ़ के साथ पावर फ़ंक्शंस को चित्रित करें y = x a जब a = 11 12 (ग्राफिक रंग काला); ए = 5 7 (ग्राफ़ का लाल रंग); ए = 1 3 (ग्राफ़ का नीला रंग); a = 2 5 (ग्राफ़ का हरा रंग)।

घातांक a के अन्य मान (0 प्रदान किए गए)< a < 1) дадут аналогичный вид графика.

परिभाषा 10

0 पर पावर फ़ंक्शन के गुण< a < 1:

• रेंज: y ∈ [ 0 ; + ∞) ;
• x ∈ [ 0 ; के लिए फलन बढ़ रहा है; + ∞) ;
• फ़ंक्शन x ∈ (0 ; + ∞) के लिए उत्तल है;
• कोई विभक्ति बिंदु नहीं हैं;
• कोई स्पर्शोन्मुख नहीं हैं;

आइए पावर फ़ंक्शन का विश्लेषण करें y = x a, जब घातांक एक गैर-पूर्णांक परिमेय या अपरिमेय संख्या है, बशर्ते कि a > 1.

आइए हम पावर फ़ंक्शन को ग्राफ़ के साथ चित्रित करें उदाहरण के रूप में निम्नलिखित कार्यों का उपयोग करते हुए दी गई शर्तों के तहत y = x a: y = x 5 4 , y = x 4 3 , y = x 7 3 , y = x 3 π (ग्राफ़ का काला, लाल, नीला, हरा रंग, क्रमश)।

घातांक a के अन्य मान, बशर्ते a > 1, एक समान ग्राफ देगा।

परिभाषा 11

> 1 के लिए पावर फ़ंक्शन के गुण:

• परिभाषा का क्षेत्र: x ∈ [ 0 ; + ∞) ;
• रेंज: y ∈ [ 0 ; + ∞) ;
• यह फ़ंक्शन सामान्य रूप का फ़ंक्शन है (यह न तो विषम है और न ही सम);
• x ∈ [ 0 ; के लिए फलन बढ़ रहा है; + ∞) ;
• फ़ंक्शन में x ∈ (0 ; + ∞) के लिए अवतलता है (जब 1< a < 2) и выпуклость при x ∈ [ 0 ; + ∞) (когда a > 2);
• कोई विभक्ति बिंदु नहीं हैं;
• कोई स्पर्शोन्मुख नहीं हैं;
• फ़ंक्शन के पासिंग पॉइंट: (0 ; 0) , (1 ; 1) .

कृपया ध्यान दें! जब एक विषम हर के साथ एक नकारात्मक अंश होता है, तो कुछ लेखकों के कार्यों में यह राय होती है कि इस मामले में परिभाषा का क्षेत्र अंतराल है - ∞; 0 ∪ (0 ; + ∞) इस चेतावनी के साथ कि घातांक a एक अपरिवर्तनीय भिन्न है। फिलहाल, बीजगणित और विश्लेषण के सिद्धांतों पर शैक्षिक सामग्री के लेखक तर्क के नकारात्मक मूल्यों के लिए एक विषम हर के साथ एक अंश के रूप में एक घातांक के साथ शक्ति कार्यों को परिभाषित नहीं करते हैं। इसके अलावा, हम बिल्कुल इसी दृष्टिकोण का पालन करते हैं: हम सेट (0 ; + ∞) को आंशिक नकारात्मक घातांक के साथ पावर फ़ंक्शन की परिभाषा के क्षेत्र के रूप में लेते हैं। छात्रों के लिए अनुशंसा: असहमति से बचने के लिए इस बिंदु पर अपने शिक्षक का दृष्टिकोण स्पष्ट करें।

आइए विषय को जारी रखें और पावर फ़ंक्शन का विश्लेषण करें y = x a प्रदान किया गया:- 1< a < 0 .

आइए हम निम्नलिखित कार्यों के ग्राफ़ का एक चित्र प्रस्तुत करें: y = x - 5 6, y = x - 2 3, y = x - 1 2 2, y = x - 1 7 (काला, लाल, नीला, हरा रंग) पंक्तियाँ, क्रमशः)।

परिभाषा 12

पावर फ़ंक्शन के गुण - 1< a < 0:

lim x → 0 + 0 x a = + ∞ जब - 1< a < 0 , т.е. х = 0 – вертикальная асимптота;

• रेंज: y ∈ 0 ; + ∞ ;
• यह फ़ंक्शन सामान्य रूप का फ़ंक्शन है (यह न तो विषम है और न ही सम);
• कोई विभक्ति बिंदु नहीं हैं;

नीचे दिया गया चित्र पावर फ़ंक्शंस y = x - 5 4, y = x - 5 3, y = x - 6, y = x - 24 7 (वक्रों के क्रमशः काले, लाल, नीले, हरे रंग) के ग्राफ़ दिखाता है।

परिभाषा 13

ए के लिए पावर फ़ंक्शन के गुण< - 1:

• परिभाषा का क्षेत्र: x ∈ 0 ; + ∞ ;

lim x → 0 + 0 x a = + ∞ जब a< - 1 , т.е. х = 0 – вертикальная асимптота;

• रेंज: y ∈ (0 ; + ∞) ;
• यह फ़ंक्शन सामान्य रूप का फ़ंक्शन है (यह न तो विषम है और न ही सम);
• x ∈ 0 के लिए फलन घट रहा है; + ∞ ;
• फ़ंक्शन में x ∈ 0 के लिए अवतलता है; + ∞ ;
• कोई विभक्ति बिंदु नहीं हैं;
• क्षैतिज अनन्तस्पर्शी - सीधी रेखा y = 0;
• फ़ंक्शन के पारित होने का बिंदु: (1; 1) .

जब a = 0 और x ≠ 0, हम फ़ंक्शन y = x 0 = 1 प्राप्त करते हैं, जो उस रेखा को परिभाषित करता है जिसमें से बिंदु (0; 1) को बाहर रखा गया है (यह सहमति थी कि अभिव्यक्ति 0 0 को कोई अर्थ नहीं दिया जाएगा ).

घातांकीय फलन का रूप होता है y = a x, जहां a > 0 और a ≠ 1, और इस फ़ंक्शन का ग्राफ़ आधार a के मान के आधार पर भिन्न दिखता है। आइए विशेष मामलों पर विचार करें.

सबसे पहले, आइए उस स्थिति को देखें जब घातीय फलन के आधार का मान शून्य से एक (0) हो< a < 1) . एक अच्छा उदाहरण a = 1 2 (वक्र का नीला रंग) और a = 5 6 (वक्र का लाल रंग) के लिए फ़ंक्शन का ग्राफ़ है।

घातीय फ़ंक्शन के ग्राफ़ में शर्त 0 के तहत आधार के अन्य मानों के लिए समान उपस्थिति होगी< a < 1 .

परिभाषा 14

जब आधार एक से कम हो तो घातांकीय फलन के गुण:

• रेंज: y ∈ (0 ; + ∞) ;
• यह फ़ंक्शन सामान्य रूप का फ़ंक्शन है (यह न तो विषम है और न ही सम);
• एक घातीय फ़ंक्शन जिसका आधार एक से कम है, परिभाषा के पूरे क्षेत्र में घट रहा है;
• कोई विभक्ति बिंदु नहीं हैं;
• क्षैतिज अनंतस्पर्शी - सीधी रेखा y = 0 जिसमें चर x + ∞ की ओर प्रवृत्त है;

अब उस मामले पर विचार करें जब घातांकीय फलन का आधार एक (a > 1) से बड़ा है।

आइए इस विशेष मामले को घातीय फलनों y = 3 2 x (वक्र का नीला रंग) और y = e x (ग्राफ का लाल रंग) के ग्राफ के साथ चित्रित करें।

आधार के अन्य मान, बड़ी इकाइयाँ, घातीय फ़ंक्शन के ग्राफ़ को समान रूप देंगी।

परिभाषा 15

जब आधार एक से बड़ा हो तो घातांकीय फलन के गुण:

• परिभाषा का क्षेत्र - वास्तविक संख्याओं का संपूर्ण सेट;
• रेंज: y ∈ (0 ; + ∞) ;
• यह फ़ंक्शन सामान्य रूप का फ़ंक्शन है (यह न तो विषम है और न ही सम);
• एक घातांकीय फलन जिसका आधार एक से बड़ा है x ∈ - ∞ के रूप में बढ़ रहा है; + ∞ ;
• फ़ंक्शन में x ∈ - ∞ पर अवतलता है; + ∞ ;
• कोई विभक्ति बिंदु नहीं हैं;
• क्षैतिज अनंतस्पर्शी - सीधी रेखा y = 0 जिसमें चर x - ∞ की ओर प्रवृत्त है;
• फ़ंक्शन के पारित होने का बिंदु: (0; 1) .

लॉगरिदमिक फ़ंक्शन का रूप y = log a (x) है, जहां a > 0, a ≠ 1 है।

ऐसा फ़ंक्शन केवल तर्क के सकारात्मक मानों के लिए परिभाषित किया गया है: x ∈ 0 के लिए; + ∞ .

आधार a के मान के आधार पर, लॉगरिदमिक फ़ंक्शन के ग्राफ़ का स्वरूप भिन्न होता है।

आइए पहले उस स्थिति पर विचार करें जब 0< a < 1 . Продемонстрируем этот частный случай графиком логарифмической функции при a = 1 2 (синий цвет кривой) и а = 5 6 (красный цвет кривой).

आधार के अन्य मान, बड़ी इकाइयाँ नहीं, समान प्रकार का ग्राफ़ देंगे।

परिभाषा 16

जब आधार एक से कम हो तो लघुगणकीय फ़ंक्शन के गुण:

• परिभाषा का क्षेत्र: x ∈ 0 ; + ∞ . जैसे ही x दाईं ओर से शून्य की ओर जाता है, फ़ंक्शन मान +∞ की ओर प्रवृत्त होते हैं;
• मानों की सीमा: y ∈ - ∞ ; + ∞ ;
• यह फ़ंक्शन सामान्य रूप का फ़ंक्शन है (यह न तो विषम है और न ही सम);
• लघुगणक
• फ़ंक्शन में x ∈ 0 के लिए अवतलता है; + ∞ ;
• कोई विभक्ति बिंदु नहीं हैं;
• कोई स्पर्शोन्मुख नहीं हैं;

आइए अब उस विशेष मामले को देखें जब लघुगणकीय फ़ंक्शन का आधार एक से अधिक हो: a > 1 . नीचे दिया गया चित्र लॉगरिदमिक फ़ंक्शंस y = log 3 2 x और y = ln x (क्रमशः ग्राफ़ के नीले और लाल रंग) के ग्राफ़ दिखाता है।

एक से अधिक आधार के अन्य मान भी इसी प्रकार का ग्राफ देंगे।

परिभाषा 17

जब आधार एक से बड़ा हो तो लघुगणकीय फ़ंक्शन के गुण:

• परिभाषा का क्षेत्र: x ∈ 0 ; + ∞ . चूँकि x दाईं ओर से शून्य की ओर प्रवृत्त होता है, फ़ंक्शन मान - ∞ की ओर प्रवृत्त होते हैं;
• मानों की सीमा: y ∈ - ∞ ; + ∞ (वास्तविक संख्याओं का पूरा सेट);
• यह फ़ंक्शन सामान्य रूप का फ़ंक्शन है (यह न तो विषम है और न ही सम);
• x ∈ 0 के लिए लघुगणक फलन बढ़ रहा है; + ∞ ;
• फ़ंक्शन x ∈ 0 के लिए उत्तल है; + ∞ ;
• कोई विभक्ति बिंदु नहीं हैं;
• कोई स्पर्शोन्मुख नहीं हैं;
• फ़ंक्शन के पारित होने का बिंदु: (1; 0) .

त्रिकोणमितीय फलन साइन, कोसाइन, स्पर्शरेखा और कोटैंजेंट हैं। आइए उनमें से प्रत्येक के गुणों और संबंधित ग्राफिक्स को देखें।

सामान्य तौर पर, सभी त्रिकोणमितीय कार्यों को आवधिकता की संपत्ति द्वारा विशेषता दी जाती है, यानी। जब फ़ंक्शन के मान तर्क के विभिन्न मानों के लिए दोहराए जाते हैं, तो अवधि f (x + T) = f (x) (T अवधि है) द्वारा एक दूसरे से भिन्न होते हैं। इस प्रकार, आइटम "सबसे छोटा सकारात्मक अवधि" त्रिकोणमितीय कार्यों के गुणों की सूची में जोड़ा जाता है। इसके अलावा, हम उस तर्क के मानों को इंगित करेंगे जिस पर संबंधित फ़ंक्शन शून्य हो जाता है।

1. ज्या फलन: y = पाप(x)

इस फ़ंक्शन के ग्राफ़ को साइन वेव कहा जाता है।

परिभाषा 18

साइन फ़ंक्शन के गुण:

• परिभाषा का क्षेत्र: वास्तविक संख्याओं का संपूर्ण सेट x ∈ - ∞ ; + ∞ ;
• फ़ंक्शन गायब हो जाता है जब x = π · k, जहां k ∈ Z (Z पूर्णांकों का समुच्चय है);
• फ़ंक्शन x ∈ - π 2 + 2 π · k के लिए बढ़ रहा है; π 2 + 2 π · k, k ∈ Z और x ∈ π 2 + 2 π · k के लिए घट रहा है; 3 π 2 + 2 π · के, के ∈ जेड;
• साइन फलन में बिंदु π 2 + 2 π · k पर स्थानीय उच्चिष्ठ होता है; 1 और बिंदुओं पर स्थानीय न्यूनतम - π 2 + 2 π · k; - 1, के ∈ जेड;
• साइन फलन अवतल होता है जब x ∈ - π + 2 π · k ; 2 π · k, k ∈ Z और उत्तल जब x ∈ 2 π · k; π + 2 π k, k ∈ Z;
• कोई स्पर्शोन्मुख नहीं हैं.

1. कोसाइन फ़ंक्शन: y = cos(x)

इस फ़ंक्शन के ग्राफ़ को कोसाइन तरंग कहा जाता है।

परिभाषा 19

कोसाइन फ़ंक्शन के गुण:

• परिभाषा का क्षेत्र: x ∈ - ∞ ; + ∞ ;
• सबसे छोटी सकारात्मक अवधि: टी = 2 π;
• मानों की सीमा: y ∈ - 1 ; 1 ;
• यह फ़ंक्शन सम है, क्योंकि y (- x) = y (x);
• फ़ंक्शन x ∈ - π + 2 π · k के लिए बढ़ रहा है; 2 π · k, k ∈ Z और x ∈ 2 π · k के लिए घट रहा है; π + 2 π k, k ∈ Z;
• कोसाइन फलन में बिंदु 2 π · k पर स्थानीय उच्चिष्ठ होता है; 1, k ∈ Z और बिंदुओं पर स्थानीय न्यूनतम π + 2 π · k; - 1, के ∈ जेड;
• कोज्या फलन अवतल होता है जब x ∈ π 2 + 2 π · k ; 3 π 2 + 2 π · k , k ∈ Z और उत्तल जब x ∈ - π 2 + 2 π · k ; π 2 + 2 π · के, के ∈ जेड;
• विभक्ति बिंदुओं के निर्देशांक π 2 + π · k हैं; 0 , k ∈ Z
• कोई स्पर्शोन्मुख नहीं हैं.

1. स्पर्शरेखा कार्य: वाई = टी जी (एक्स)

इस फ़ंक्शन का ग्राफ़ कहा जाता है स्पर्शरेखा

परिभाषा 20

स्पर्शरेखा फलन के गुण:

• परिभाषा का क्षेत्र: x ∈ - π 2 + π · k ; π 2 + π · k, जहां k ∈ Z (Z पूर्णांकों का समुच्चय है);
• परिभाषा के क्षेत्र की सीमा पर स्पर्शरेखा फलन का व्यवहार lim x → π 2 + π · k + 0 t g (x) = - ∞ , lim x → π 2 + π · k - 0 t g (x) = + ∞ . इस प्रकार, सीधी रेखाएँ x = π 2 + π · k k ∈ Z ऊर्ध्वाधर अनंतस्पर्शी रेखाएँ हैं;
• जब k ∈ Z के लिए x = π · k होता है तो फ़ंक्शन गायब हो जाता है (Z पूर्णांकों का समुच्चय है);
• मानों की सीमा: y ∈ - ∞ ; + ∞ ;
• यह फ़ंक्शन अजीब है, क्योंकि y (- x) = - y (x) ;
• फलन इस प्रकार बढ़ रहा है - π 2 + π · k ; π 2 + π · के, के ∈ जेड;
• x ∈ [π·k; के लिए स्पर्श रेखा फलन अवतल है; π 2 + π · k) , k ∈ Z और x ∈ (- π 2 + π · k ; π · k ] , k ∈ Z ; के लिए उत्तल;
• विभक्ति बिंदुओं के निर्देशांक होते हैं π · k ; 0 , क ∈ जेड ;

1. कोटैंजेंट फ़ंक्शन: वाई = सी टी जी (एक्स)

इस फ़ंक्शन के ग्राफ़ को कोटैंजेंटॉइड कहा जाता है। .

परिभाषा 21

कोटैंजेंट फ़ंक्शन के गुण:

• परिभाषा का क्षेत्र: x ∈ (π · k ; π + π · k) , जहां k ∈ Z (Z पूर्णांकों का समुच्चय है);

परिभाषा के क्षेत्र की सीमा पर कोटैंजेंट फ़ंक्शन का व्यवहार lim x → π · k + 0 t g (x) = + ∞ , lim x → π · k - 0 t g (x) = - ∞ . इस प्रकार, सीधी रेखाएँ x = π · k k ∈ Z ऊर्ध्वाधर अनंतस्पर्शी रेखाएँ हैं;

• सबसे छोटी सकारात्मक अवधि: टी = π;
• फ़ंक्शन गायब हो जाता है जब x = π 2 + π · k for k ∈ Z (Z पूर्णांकों का समुच्चय है);
• मानों की सीमा: y ∈ - ∞ ; + ∞ ;
• यह फ़ंक्शन अजीब है, क्योंकि y (- x) = - y (x) ;
• x ∈ π · k के लिए फलन घट रहा है; π + π k, k ∈ Z;
• कोटैंजेंट फ़ंक्शन x ∈ (π · k; π 2 + π · k ], k ∈ Z के लिए अवतल है और x ∈ [ - π 2 + π · k ; π · k), k ∈ Z के लिए उत्तल है;
• विभक्ति बिंदुओं के निर्देशांक π 2 + π · k हैं; 0 , क ∈ जेड ;
• कोई तिरछा या क्षैतिज अनंतस्पर्शी नहीं हैं।

व्युत्क्रम त्रिकोणमितीय फलन आर्कसाइन, आर्ककोसाइन, आर्कटैन्जेंट और आर्ककोटैंजेंट हैं। अक्सर, नाम में उपसर्ग "आर्क" की उपस्थिति के कारण, व्युत्क्रम त्रिकोणमितीय कार्यों को आर्क फ़ंक्शन कहा जाता है .

1. चाप ज्या फलन: y = a r c पाप (x)

परिभाषा 22

आर्क्साइन फ़ंक्शन के गुण:

• यह फ़ंक्शन अजीब है, क्योंकि y (- x) = - y (x) ;
• आर्क्साइन फ़ंक्शन में x ∈ 0 के लिए अवतलता है; 1 और x ∈ - 1 के लिए उत्तलता; 0 ;
• विभक्ति बिंदुओं के निर्देशांक (0; 0) होते हैं, जो फ़ंक्शन का शून्य भी है;
• कोई स्पर्शोन्मुख नहीं हैं.

1. आर्क कोसाइन फ़ंक्शन: y = a r c cos (x)

परिभाषा 23

आर्क कोसाइन फ़ंक्शन के गुण:

• परिभाषा का क्षेत्र: x ∈ - 1 ; 1 ;
• रेंज: y ∈ 0 ; π;
• यह फ़ंक्शन सामान्य रूप का है (न तो सम और न ही विषम);
• फ़ंक्शन परिभाषा के संपूर्ण क्षेत्र में घट रहा है;
• आर्क कोसाइन फ़ंक्शन में x ∈ - 1 पर अवतलता होती है; 0 और x ∈ 0 के लिए उत्तलता; 1 ;
• विभक्ति बिंदुओं के निर्देशांक 0 हैं; π 2;
• कोई स्पर्शोन्मुख नहीं हैं.

1. आर्कटिक फलन: y = a r c t g (x)

परिभाषा 24

आर्कटेंजेंट फ़ंक्शन के गुण:

• परिभाषा का क्षेत्र: x ∈ - ∞ ; + ∞ ;
• मानों की सीमा: y ∈ - π 2 ; π 2;
• यह फ़ंक्शन अजीब है, क्योंकि y (- x) = - y (x) ;
• फ़ंक्शन परिभाषा के संपूर्ण क्षेत्र में बढ़ रहा है;
• आर्कटेंजेंट फ़ंक्शन में x ∈ (- ∞ ; 0 ] के लिए अवतलता और x ∈ [ 0 ; + ∞) के लिए उत्तलता है;
• विभक्ति बिंदु में निर्देशांक (0; 0) हैं, जो फ़ंक्शन का शून्य भी है;
• क्षैतिज अनंतस्पर्शी सीधी रेखाएं हैं y = - π 2 जैसा कि x → - ∞ और y = π 2 है क्योंकि x → + ∞ (आकृति में, अनंतस्पर्शी रेखाएं हरी रेखाएं हैं)।

1. चाप स्पर्शरेखा फ़ंक्शन: y = a r c c t g (x)

परिभाषा 25

आर्ककोटैंजेंट फ़ंक्शन के गुण:

• परिभाषा का क्षेत्र: x ∈ - ∞ ; + ∞ ;
• रेंज: y ∈ (0; π) ;
• यह फ़ंक्शन सामान्य रूप का है;
• फ़ंक्शन परिभाषा के संपूर्ण क्षेत्र में घट रहा है;
• चाप कोटैंजेंट फ़ंक्शन में x ∈ [ 0 ; के लिए अवतलता होती है; + ∞) और x ∈ (- ∞ ; 0 ] ) के लिए उत्तलता;
• विभक्ति बिंदु के निर्देशांक 0 हैं; π 2;
• क्षैतिज अनंतस्पर्शी सीधी रेखाएं हैं y = π x → - ∞ पर (चित्र में हरी रेखा) और y = 0 x → + ∞ पर।

यदि आपको पाठ में कोई त्रुटि दिखाई देती है, तो कृपया उसे हाइलाइट करें और Ctrl+Enter दबाएँ

एक जटिल चर के कार्यों पर विचार करते हुए, लिउविल ने प्राथमिक कार्यों को कुछ अधिक व्यापक रूप से परिभाषित किया। प्राथमिक कार्य यचर एक्स- विश्लेषणात्मक फ़ंक्शन, जिसे बीजगणितीय फ़ंक्शन के रूप में दर्शाया जा सकता है एक्सऔर कार्य , और कुछ बीजीय फलन का लघुगणक या घातांक है जी 1 से एक्स .

उदाहरण के लिए, पाप( एक्स) - का बीजगणितीय कार्य इ मैंएक्स .

विचार की व्यापकता को सीमित किए बिना, हम कार्यों को बीजगणितीय रूप से स्वतंत्र मान सकते हैं, अर्थात, यदि बीजगणितीय समीकरण सभी के लिए संतुष्ट है एक्स, तो बहुपद के सभी गुणांक शून्य के बराबर हैं.

प्राथमिक कार्यों का विभेदन

कहाँ जेड 1 "(जेड) बराबर या जी 1 " / जी 1 या जेड 1 जी 1" इस पर निर्भर करता है कि यह एक लघुगणक है या नहीं जेड 1 या घातांक, आदि। व्यवहार में, व्युत्पन्न तालिका का उपयोग करना सुविधाजनक है।

प्राथमिक कार्यों को एकीकृत करना

लिउविले का प्रमेय प्राथमिक कार्यों के प्रतीकात्मक एकीकरण के लिए एल्गोरिदम बनाने का आधार है, उदाहरण के लिए, में लागू किया गया

सीमा की गणना

लिउविले का सिद्धांत सीमाओं की गणना पर लागू नहीं होता है। यह ज्ञात नहीं है कि क्या कोई एल्गोरिदम है, जो प्राथमिक सूत्र द्वारा दिए गए अनुक्रम को देखते हुए उत्तर देता है कि इसकी कोई सीमा है या नहीं। उदाहरण के लिए, यह प्रश्न खुला है कि क्या अनुक्रम अभिसरित होता है।

साहित्य

• जे. लिउविल. कार्यों के पारगमन के एकीकरण का एक और वर्गीकरण// जे. रेइन एंज्यू। गणित। बी.डी. 13, पृ. 93-118. (1835)
• जे.एफ. रिट. सीमित शर्तों में एकीकरण. एन.-वाई., 1949 // http://lib.homelinux.org
• ए जी खोवांस्की। टोपोलॉजिकल गैलोज़ सिद्धांत: परिमित रूप में समीकरणों की सॉल्वैबिलिटी और अनसॉल्वैबिलिटीचौ. 1. एम, 2007

टिप्पणियाँ

विकिमीडिया फ़ाउंडेशन. 2010.

• प्राथमिक उत्तेजना
• प्राथमिक परिणाम

देखें अन्य शब्दकोशों में "प्राथमिक कार्य" क्या है:

प्राथमिक कार्य- एक फ़ंक्शन, जिसे यदि छोटे फ़ंक्शंस में विभाजित किया जाता है, तो डिजिटल ट्रांसमिशन पदानुक्रम में विशिष्ट रूप से परिभाषित नहीं किया जा सकता है। इसलिए, नेटवर्क के दृष्टिकोण से यह अविभाज्य है (आईटीयू टी जी.806)। विषय: दूरसंचार, बुनियादी अवधारणाएँ EN अनुकूलन फ़ंक्शनए... तकनीकी अनुवादक मार्गदर्शिका

नेटवर्क स्तरों के बीच अंतःक्रिया का कार्य- एक प्राथमिक कार्य जो दो नेटवर्क परतों के बीच विशिष्ट जानकारी की परस्पर क्रिया प्रदान करता है। (आईटीयू टी जी.806)। विषय: दूरसंचार, EN परत की बुनियादी अवधारणाएँ... ... तकनीकी अनुवादक मार्गदर्शिका